Print bookPrint book

Exponential Decay

Site: Gladwin
Course: Michigan Algebra I Sept. 2012
Book: Exponential Decay
Printed by: Guest user
Date: Saturday, November 23, 2024, 4:57 AM

Description

Exponential Decay

Table of contents

Introduction

In the last section, we looked at functions that model exponential growth. We saw that exponential functions describe a quantity that doubles, triples, quadruples, or gets multiplied by the same factor repeatedly. All the functions we looked at in the last section were exponentially increasing functions. They started small and then became large very quickly.

In this section, we are going to look at exponentially decreasing functions. An example of such a function is a quantity that gets decreased by one half each time. These functions are exponential decay functions.


Example 1

For her fifth birthday, Nadia's grandmother gave her a full bag of candy. Nadia counted her candy and found out that there were 160 pieces in the bag. As you might suspect Nadia loves candy so she ate half the candy on the first day. Her mother told her that if she eats it at that rate it will be all gone the next day and she will not have any more until her next birthday.

Nadia devised a clever plan. She will always eat half of the candy that is left in the bag each day. She thinks that she will get candy every day and her candy will never run out. How much candy does Nadia have at the end of the week? Would the candy really last forever?

Step 1. Determine the initial value.

Since the first day she had 160 pieces of candy, the initial value is 160.

Step 2. Determine the decay factor.

Since she is eating half the candy every day, it is being multiplied by 0.5 each day. Therefore, the decay factor is 0.5.

Step 3. Write an exponential function.

The general form of an exponential function is ExpDecayEx1-1.

For this situation, the equation is ExpDecayEx1-2.

Continued

Step 4. Answer the first question.

Since there are 7 days in a week, use 7 as the exponent.

ExpDecayEx1-3

At the end of the week, she will have 1.25 pieces of candy left.

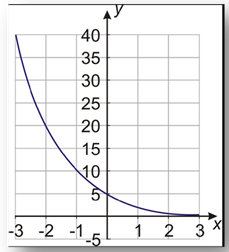
Step 5. Graph the candy problem function. Use the graph to answer the final question.

ExpDecayEx1-4

Will Nadia's candy last forever? Notice that the graph never really gets to zero, this is due to the asymptotic behavior of exponentials discussed in previous lessons. Theoretically there will always be some candy left, but she will be eating very tiny fractions of one piece of candy every day after the first week.

Graph an Exponential Decay

The graph of an exponential decay function will always take the same basic shape as the one in the previous example. It will decrease quickly in the beginning and then slower and slower. One way to make a graph of an exponential function is to make a table of values and plot points.

Example Graph the exponential function GraphDecayEx1-1

Step 1. Make a table of values.

GraphDecayEx1-9

Step 2: Graph the function by plotting points.

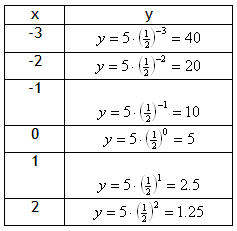
Negative Reciprocal

Remember that a whole number to a negative power is equivalent to its reciprocal to the positive power. For instance, y = 5 · 2 ?x is equivalent to NegRecip1-1. Therefore, these types of functions also create exponential decay.

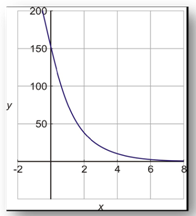
Example Graph the exponential function y = 8 · 3?x.

Step 1. Make a table of values.

NegRecip1-2
Step 2. Graph the function by plotting points.

NegRecip1-3

Growth vs. Decay

An exponential growth graph starts very small and increases very quickly and the values end up very, very large. While an exponential decay graph starts with very large values, it decreases very quickly becoming very, very small values.

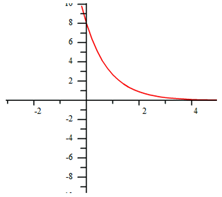
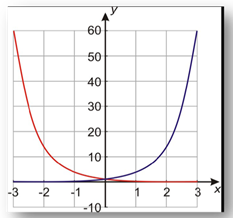
Example Graph the functions y = 4x and y = 4?x on the same coordinate axes.

Step 1. Make a table of values.

GrowthvDecayEx1-1

*Note: The values of these two functions are reciprocals of each other.

Step 2. Graph the function by plotting points.

GrowthvDecayEx1-2

*Note: The second function is a reflection of the first function across the y-axis. Recall from earlier discussions of transformations of graphs, that this is always true.

Application

Exponential decay problems appear in several application problems. Some examples of these are half-life problems, and depreciation problems.

Example 1 A radioactive substance has a half-life of one week. In other words, at the end of every week the level of radioactivity is half of its value at the beginning of the week. The initial level of radioactivity is 20 counts per second.

a) Draw the graph of the amount of radioactivity versus the time in weeks.
b) Find the formula that gives the radioactivity in terms of time.
c) Find the radioactivity left after three weeks

Step 1. Make a table of values to represent the function.

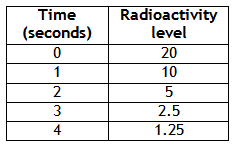RealWorld2 

Step 2. Plot the points to make a graph.

 RealWorld1

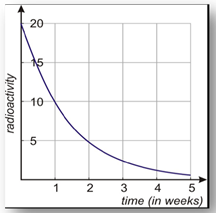
Example 1 Continued

Step 3. Write a model for the exponential decay.

Remember that the general formula for an exponential function is RealWorldEx1-1

a is the initial value, so a = 20.
b is the common ratio, so b = 1/2.

Therefore, the equation is RealWorldEx1-2

Step 4. Determine the amount of radioactivity left after three weeks.

Since x represents the number of weeks, let x = 3.

RealWorldEx1-3

Example 2

The cost of a new car is $32,000. It depreciates at a rate of 15% per year. This means that it loses 15% of each value each year.

a) Draw the graph of the car's value versus the time in years.
b) Find the formula that gives the value of the car in terms of time.
c) Find the value of the car when it is four years old.

Step 1. Make a table of values to represent the function.

RealWorldEx2-1

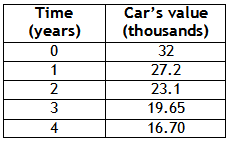
Step 2. Plot the points to make a graph.

RealWorldEx2-2

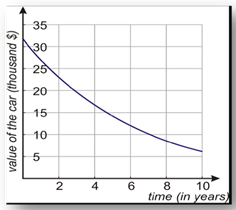
Step 3. Write a model for the exponential decay.

Remember that the general formula for an exponential function is RealWorldEx2-3

a is the initial value, so a = 32,000.

Since the car is decreasing from 100% at a rate of 15%, b = 100%-15% = 85% = 0.85.

Therefore, the equation is RealWorldEx2-4

Step 4. Determine the value of the car after four years.

Since x represents the number of years, let x = 4.

y = 32,000 · (0.85)4 = $16,704.
.

Video Lessons

To learn how to determine the formula and solution to exponential decay, select the following links:

Exponential Decay #1

Exponential Decay #2 

Exponential Decay

Guided Practice

To solidify your understanding of exponential decay, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Practice

Exponential Decay Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Exponential Decay Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Gloag, Anne & Andrew. "Exponential Functions." February 24,

2010.http://www.ck12.org/flexr/chapter/4478

Holt, Rinehart, & Winston. "Exponential & Logarithmic Functions."

http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch07_01_homeworkhelp.html (accessed September 10, 2010).