Inverses
| Site: | Gladwin |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Inverses |
| Printed by: | Guest user |
| Date: | Friday, January 16, 2026, 10:10 PM |
Description
Inverses
Introduction
Just like all families of functions, exponential functions have an inverse. To find the inverse, switch the x and y values of the graph, table or equation to see the new function.
Example Graph the inverse of the function: y = 2x.
Step 1. Make a table of values.
![]()
Step 2. Switch the values of x and y in the table.
![]()
Step 3. Plot the points on a coordinate plane.
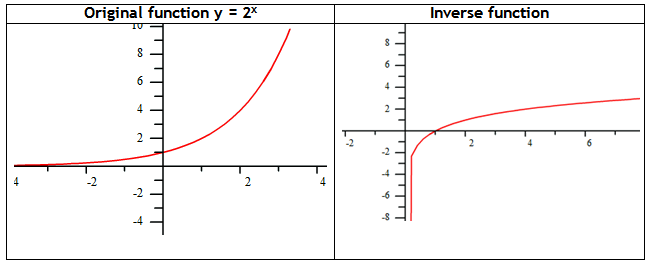
Logarithms
y = bx is equivalent to logb( y) = x
The right-hand side above is pronounced, "log-base-b of y equals x". The value of the subscripted "b" is the base of the logarithm, just as b is the base in the exponential equation. And, just as the base b of an exponential is always positive and never equal to 1, so is the base b for a logarithm.
* Note: Finding the logarithm that corresponds to the exponential function will be covered in Algebra II. Look at the following examples as a way to introduce yourself to the idea that will be covered later.
Examples
Convert 63 = 216 to the equivalent logarithmic equation.
To convert, the base remains the same, but the 3 and the 216 switch sides.
log6 (216) = 3
Example 2
Convert log4(1024) = 5 to the equivalent exponential equation.
To convert, the base remains the same, but the 1024 and the 5 switch sides.
4 5 = 1024
Video Lesson
Practice
Answer Key
Sources
Khan, Salman. " An introduction to logarithms."
http://www.khanacademy.org/video/introduction-to-logarithms (accessed September 12, 2010).
Stapel, Elizabeth. "Logarithms: Introduction to 'The Relationship'." Purplemath. Available from http://www.purplemath.com/modules/logs.htm. Accessed 12 September 2010