Power & Exponential Functions
| Site: | Gladwin |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Power & Exponential Functions |
| Printed by: | Guest user |
| Date: | Tuesday, February 17, 2026, 7:07 PM |
Description
Introduction
This unit will focus on two functions, power functions and exponential functions. They are put together because their equations look very similar, but their graphs are very different. A power function in general form is y = kxp, where k and p are constants. Some examples of power functions include:
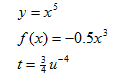
An exponential function in general form is y = abx, where a and b are constants. Since the equations are so similar, they are easy to confuse. The main difference between them is that the variable is in the exponent of the exponential function. This is the first instance where the variable has been in this position. Some examples of exponential functions include:
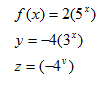
Graphs
Although the equations of power and exponential functions appear to be similar at first glance, their graphs are very different. Here are basic examples of each type of function.

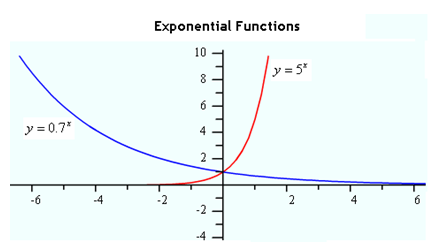
The rest of this unit will develop a deeper understanding of each of these functions, but having the basic understanding of their similarities and differences is vital to unlocking that understanding.