Print bookPrint book

Graphically

Site: Gladwin
Course: Michigan Algebra I Sept. 2012
Book: Graphically
Printed by: Guest user
Date: Thursday, November 21, 2024, 8:45 AM

Description

Graphically

Table of contents

Finding Solutions

In the study of polynomial equations, it is important to understand how to find the solution of the equation. Equations of higher degree allow for many solutions. The maximum number of solutions possible is equal to the degree of the polynomial. Graphs can be used to find the solutions of polynomial equations.

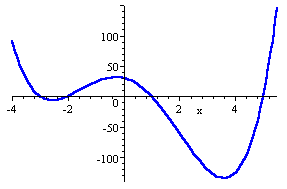
When a polynomial equation is set equal to 0, the solutions of the polynomial are the x-intercepts or roots of the corresponding graph. For example, to solve the equation, x4? x3 ? 19x2 ? 11x + 31 = 0 graphically, means to find the roots or x-intercepts of the corresponding function, f(x) = x4? x3 ? 19x2 ? 11x + 31. The graph below shows that there are 4 roots, at approximately x = -3, x = -2, x = 1, and x = 5. While these are not exact answers, they can be used to find exact answers using a table.

PolyGraphically


Example 1

By looking at the graph, how many roots does this equation have?

-x3 + 5x2 - 3x - 3 = 0

Step 1. Create the corresponding function.

PolyGraphEx1-1

Step 2. Make a graph of the function.

PolyGraphEx1-2

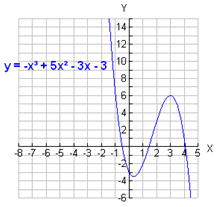
Step 3. Count the number of x-intercepts of the graph.

Since there are three x-intercepts of the graph, there are three roots of the equation.

Example 2

What are the zeros of this polynomial function, P(x) = -x4 - 3x3 + 6x2 + 8x?

PolyGraphEx2-1

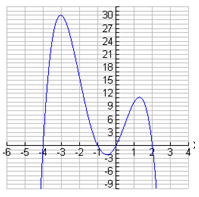
Step 1. Estimate the x-intercepts of the graph.

It appears that the zeros of the function are x = -4, x = -1, x = 0, and x = 2.

Step 2. Check the estimates by substituting into the equation.

PolyGraphEx2-2

Because the point is (-4, 0), x = -4 is an x-intercept, or zero, of the equation.

Check the remaining values to ensure accuracy.

PolyGraphEx2-3b

The zeros of the function are x = -4, x = -1, x = 0, and x = 2.

Example 3

What can be said about the degree of the polynomial P(x) depicted below?

PolyGraphEx3-1

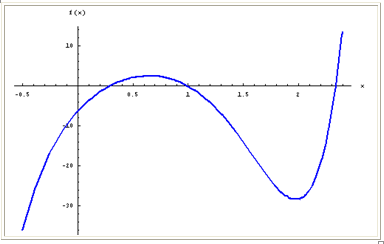
Step 1. Count the number of x-intercepts of the graph.

The graph has three x-intercepts.

Step 2. Make a statement about the comparison between the x-intercepts of the graph and the degree of the corresponding polynomial.

Since the number of x -intercepts is always equal to or less than the degree of the polynomial, this function is at least a third degree polynomial. However, it could also be a polynomial of any degree greater than three.

Interactive Activities

To learn more about the graphs of cubic polynomials, please select the following link:

Cubic Polynomial Graphs

To learn more about the characteristics of polynomial graphs, select the following link:

Characteristics of Polynomial Graphs

Repeated Zeros

When solving polynomial equations, factoring may be used. If the factor (x ? r) occurs more than once in the factorization of a function, then r is called a repeated zero, or multiple zero.

For information about repeated zeros, select the following link:

Repeated Zeros


*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Practice

Finding Zeros Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Finding Zeros Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Analyze Math, "Cubing Functions." http://www.analyzemath.com/function/cubing_function.html (accessed 8/15/10).

Analyze Math, "Polynomial Functions." http://www.analyzemath.com/ function/ polynomial2/polynomial2.htm (accessed 8/15/10).

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Interactive Math, "Polynomial Functions and Equations." http://www.intmath.com/EqnsHiDe/1_Polynomials.php (accessed 8/13/10).

"Practice with Graphs." http://www.regentsprep.org/Regents/math/algtrig/ATE13/HighGraphsPractice.htm (accessed 8/15/10).

SOS Math, "Finding Roots." http://www.sosmath.com/algebra/factor/fac03a2/fac03a2.html (accessed 8/15/10).