Print bookPrint book

Foundations

Site: Gladwin
Course: Michigan Algebra I Sept. 2012
Book: Foundations
Printed by: Guest user
Date: Saturday, November 23, 2024, 4:54 AM

Description

Foundations

Table of contents

Introduction

In general the graph of a quadratic equation, y = ax2 + bx + c, is called a parabola which is a U-shaped graph. The axis of symmetry is a vertical line through the vertex of the parabola. All parabolas are symmetric with respect to their axis of symmetry. The vertex of a parabola will be either the minimum or maximum point of the parabola, depending on whether the graph opens upward or downward.

Foundations1

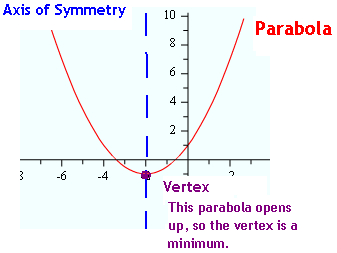
Graphing a Quadratic

To sketch the graph of a quadratic equation, follow these steps:
  • Find a, b, and c of the equation.
  • Check if a > 0 or a < 0 to decide if the graph opens up (a > 0) or down (a < 0).
  • Find the vertex. This is the minimum or maximum point of the parabola. The x-coordinate can be found by the equation 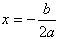GraphQuad . Once found, substitute this value into the original equation to find the value of y. These will be the (x,y) coordinates of the vertex.
  • Find the y-intercept by substituting 0 in for x in the equation.
  • Find the x-intercepts by substituting y = 0 and solving the quadratic equation. Use either the quadratic formula, completing the square, or put the equation in factored form to solve for x.

Example

Graph the quadratic equation y = 2x2 ? 8x + 6.

Step 1. Determine a, b and c and decide if the graph will open up or down.

a = 2, b= -8, and c = 6. Because a is positive, the graph will open upward.

Step 2. Find the vertex.

GraphQuadEx1-1

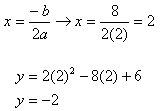
The vertex is at the point (2, -2)

Step 3. Find the x-intercepts.

To find the x-intercepts, substitute 0 in for the y and solve. This was covered completely in the solving book.

2x2 ? 8x + 6 = 0

2(x2 - 4x +3) = 0

2(x - 1)(x -3) = 0

x = 1 or x = 3

The x-intercepts are (1,0) and (3,0).

Example Continued

Step 4. Find the y-intercept.

To find the y-intercept, substitute 0 in for x and solve.
y = 2(0)2- 8(0) + 6 = 6.
The graph crosses the y-axis at the point (0,6).

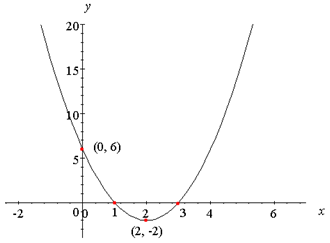
Step 5. Plot all points and connect in a "U" shaped curve to create a graph.

The graph of y = 2x2 ? 8x + 6 is:

GraphQuadEx1-2


Video Lesson

To learn how to graph quadratic functions, select the following link:

Graphing Quadratic Functions

Interactive Activities

To learn more about graphing quadratic equations, select one of the following links:

Graphing Quadratics #1

Graphing Quadratics #2

Graphing Quadratics #3

Guided Practice

To solidify your understanding of the characteristics and graphs of quadratics, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice #1

Guided Practice #2

Guided Practice #3

Sources

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Holt, Rinehart & Winston, "Quadratic Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch05_02_homeworkhelp.html (accessed 8/18/2010).

Holt, Rinehart & Winston, "Quadratic Functions and Equations." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg1/player.html?contentSrc=6373/6373.xml (accessed 8/18/2010).

Holt, Rinehart & Winston, "Quadratic Functions and Equations." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch09_04_homeworkhelp.html (accessed 8/18/2010).

Hot Math, "Graphing Quadratic Equations." http://hotmath.com/hotmath_help/topics/graphing-quadratic-equations.html (accessed 07/25/2010).

Mathematics Education Department, University of Georgia. "Intermath: Dictionary." http://intermath.coe.uga.edu/dictnary/related.asp?termid=414 (accessed 07/15/2010).

Zona Land, "Polynomial Function of the Second Degree." http://zonalandeducation.com/mmts/functionInstitute/polynomialFunctions/graphs/degree2PolynomialFunction.html (accessed 07/25/2010).