Function Notation
| Site: | Gladwin |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Function Notation |
| Printed by: | Guest user |
| Date: | Saturday, January 17, 2026, 9:28 AM |
Description
Introduction
Until this point, all graphs have come from an equation that contains an x and a y variable. These variables indicate the input and output values and correspond to the x and y-axes. Now, functions will be modeled using a new notation.
For functions, "y =" and "f(x) =" (pronounced "f-of-x") mean the exact same thing. However, "f( x)" allows for more flexibility and more information. Instead of saying "y = 2x + 3; solve for y when x = -1", the new notation says "f(x) = 2x + 3; find f(-1)". In either case, the same thing needs to be done: substitute -1 for x, multiply by 2, and then add 3, simplifying to get an output value of 1. Using the first notation, the final statement becomes; when x = -1 then y = 1. In the second notation, this would be written f(-1) = 1.
Function notation allows greater flexibility than using just "y" for every formula. Graphing calculators will list different functions as y1, y2, etc. Textbooks use names like f(x), g(x), h(t), s(t), etc. With this notation, more than one function at a time can be used without confusing or mixing up the formulas.
Writing Function Notation
A linear function can be written in the form ![]() where
where ![]() represents the output values of the equation or the y-values of the graph. The terms y and f(x) are often used interchangeably. For instance, the expression
represents the output values of the equation or the y-values of the graph. The terms y and f(x) are often used interchangeably. For instance, the expression ![]() clearly shows that x is the independent variable. The values for the dependent variable, y, are calculated when values for x are substituted into the function.
clearly shows that x is the independent variable. The values for the dependent variable, y, are calculated when values for x are substituted into the function.
Function notation is a very compact way of providing information. For example in the function f(3) = 6, the value inside the parentheses is the x value and the value the function equals is the dependent or y value. These two values yield an ordered pair that can be used for graphing the points on the line represented by the function.
Therefore, f(3) = 6 states when x = 3, then y = 6 or that the point (3, 6) is on the line. Review the table of values for both functions below:

Since both tables are the same, then f(x) = 2x is equivalent to y = 2x.
Evaluating
Evaluating a function is the process of substituting a value for the independent variable and simplifying the resulting numerical expression.
Example 1
Consider the linear function f(x) = 3x - 4. Find f(2).
Step 1. Substitute the given value of 2 for x.
f (2) = 3(2) - 4
Step 2. Follow the Order of Operations to simplify.
3(2) - 4
6 - 4
2
f (2) = 2
Example 2
Evaluate f(2x-1) = 3x - 4.
Step 1. Substitute the contents of the parentheses for x.
f (2x-1) = 3(2x-1) - 4
Step 2. Use the Distributive Property.
3?2x + 3?(-1) - 4
Step 3. Simplify.
6x - 3 - 4
6x - 7
f (2x-1) = 6x - 7
Combining Functions
When two or more functions are given, new functions can be formed by combining them. Functions can be added, subtracted, multiplied or divided. If f(x) represents one function and g(x) represents a second function, then the operations on functions may be performed as follows:
Sum of functions: ![]()
Difference of functions: ![]()
Product of functions: ![]()
Quotient of functions: 
Examples
Example 1
Given f(x) = 3x +5 and g(x) = 5x - 2 find (f + g)(x)
(3x +5) + (5x - 2)
Step 2. Combine like terms to simplify.
(f + g)(x) = 8x + 3
Example 2
Given h(x) = 3x + 4 and k(x) = 1 - 2x find (h - k)(x).
Step 1. Substitute the functions in the difference rule.
(3x + 4 ) - (1 - 2x)
Step 2. Use Distributive Property to eliminate the parentheses.
3x + 4 -1 + 2x
Step 3. Combine like terms to simplify.
(h - k)(x) = 5x + 3
Examples Continued
Example 3
Given f(x) = 2x - 1 and g(x) = 3 find (f ? g)(x).
Step 1. Substitute the functions in the product rule.
(2x - 1) (3)
Step 2. Use Distributive Property to simplify.
(f ? g)(x) = 6x - 3
Example 4
Given f(x) = 3x and g(x) = 4x - 1 find 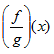 .
.
Step 1. Substitute the functions in the quotient rule.
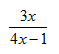
Step 2. Simplify if possible, state undefined values.
Since this expression cannot be simplified, 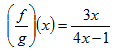 .
.
Since division by zero is undefined, ![]() .
.
Function Operations
Functions operations can be evaluated with either values of the domain or expressions.
Example 1 Given that f(x) = 3x + 2, find f(x + h) - f(h).
Step 1 . Evaluate f(x + h).
f () = 3( ) + 2
f (x + h) = 3(x + h) + 2
f(x + h)=3x+3h+ 2
Step 2. Evaluate f(h)
f () = 3( ) + 2
f (h) = 3h + 2
Step 3 . Subtract and simplify. Substitute the above expressions using the subtraction rule and combine like terms.
f (x + h) - f(h)
[3x + 3h+ 2] - [3h + 2]
3x+ 3h+ 2- 3h - 2
3x + 6h
f(x + h) - f(h) = 3x + 6h
Example 2
Given f(x) = 2x and g(x) = x + 4, find (f + g)(2).
Step 1. Evaluate each function for the given value of 2.
f (2) = 2(2) = 4
g (2) = (2) + 4 = 6
Step 2 . Evaluate the function operation using the answers above.
(f + g)(2) = f(2) + g(2) = 4 + 6 = 10
Video Lesson
Practice
Answers
Sources
Gloag, Anne and Andrew. "Writing Linear Equations", ." December 9, 2009.http://www.ck12.org/flexr/flexbook/738
Stapel, Elizabeth. "Function Notation: Introduction / Evaluation." Purplemath. Available from http://www.purplemath.com/modules/fcnnot.htm. Accessed 03 August 2010