Absolute Value
Introduction
The absolute value of x, denoted "|x|" and read "the absolute value of x", is the distance x is from zero on a number line. This is why absolute value is never negative; absolute value asks "how far?" not "in which direction?" For instance, 4 and -4 have the same absolute value of 4:
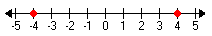
So, the absolute value of a positive number is the number itself, and the absolute value of a negative number is its opposite. The absolute value of zero is 0.
The absolute value bars do not work in the same way as do parentheses. Where -(-3) = +3, this is not true in -|-3|. To simplify -|-3| first simplify the absolute value part. The distance -3 is from zero is 3 units so the absolute value of -3 is 3, so -|-3| = - (+3) = -3.
So, the absolute value of a positive number is the number itself, and the absolute value of a negative number is its opposite. The absolute value of zero is 0.
The absolute value bars do not work in the same way as do parentheses. Where -(-3) = +3, this is not true in -|-3|. To simplify -|-3| first simplify the absolute value part. The distance -3 is from zero is 3 units so the absolute value of -3 is 3, so -|-3| = - (+3) = -3.